To prove Newton's second Law

Using Fletcher's Trolley

Thomas O’Sullivan’s Leaving Cert. Maths & Physics Notes.

Experiment: To show that the acceleration of a body is proportional to the applied force and inversely proportional to the mass of the body.

Apparatus: As in diagram:

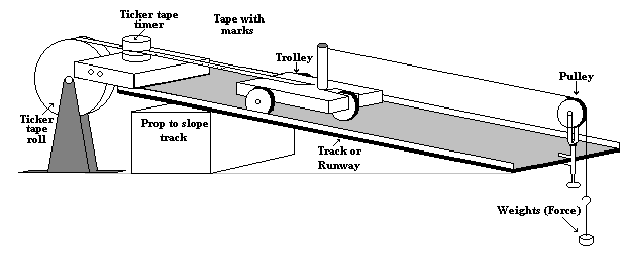
Theory:

Newton's Second law states that "the rate of change of momentum of a body is proportional to the force causing it and takes place in the direction of that force".

i.e. (mv - mu) / t µ F or m(v - u) / t µ F which gives ma µ F.

Outline of experimental procedure:

This experiment is divided into two parts.

Experiment A: To show that a µ F.

  1. Set up the apparatus as in the diagram. (The ticker tape timer is a device that puts 50 dots per second onto a long narrow piece of paper that passes over a marking device (rather like a pencil moving up and down 50 times a second)).

  2. The runway is then tilted until such time as the trolley moves with a uniform velocity (i.e. doesn't speed up) when given a small push. This means that a component of the weight of the trolley is being used to overcome the (dynamic) frictional force between the trolley and the track.

    3.  

  3. A force of 0.1 N (i.e. a mass of 100g) is placed on the scale pan and this causes the trolley to accelerate down the track.

4. As the trolley moves, the ticker tape, which is attached to it, passes through the ticker tape timer and the resultant dots can be used to find the acceleration.

To calculate the acceleration:

  1. Select two sets of five dots at either end of the tape and number them 0, 1, 2, 3 and 4 (diagram). The time for the trolley to travel the distance between dot 1 and dot 4 is 4(1/50) s.
  2. The distance between the dots can be measured with a metre stick. The average velocity (taken as the instantaneous velocity at dot 2) is calculated from speed = distance / time. This method can be used to find the initial velocity (u) and the final velocity (v). To find the acceleration the number of dots between u and v is counted and this multiplied by 1 / 50s gives the time between u and v. The acceleration can then be found from the formula v = u + at.

5. Repeat steps 3 and 4 for forces of 0.2N, 0.3N, etc..

Results:

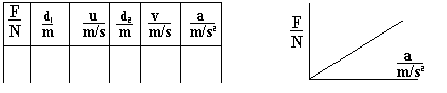
Conclusion: A straight-line graph shows that F is directly proportional to a. (the slope of this graph actually gives us the mass of the trolley.)

Experiment B. The second part of this experiment is to show that a µ1 / m.

  1. Set up the apparatus as before.

  2. Tilt runway as before.
  3. A force of 0.5N is placed in the pan. N.B. this does not change during the experiment.
  4. Find the mass of the trolley.
  5. Allow trolley to move and find its acceleration as before.
  6. Change the mass of the trolley by adding extra masses to it (say 0.1kg, 0.2kg, 0.3kg etc.) and repeat steps 4 and 5.

 

Results:

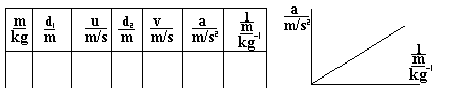
Conclusion: A straight-line graph shows that a is inversely proportional to the mass. (The slope of this graph gives us the weight in the scale pan (0.5N above)).

From parts A and B of this experiment we can deduce that F µ ma.

 

 

Note:

Tilting track to overcome friction

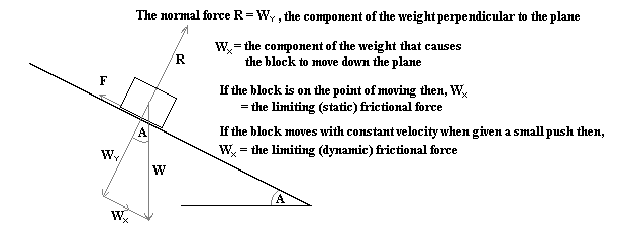
If the track is tilted then a component of the body's weight, Wx acts down the slope in the opposite direction to F, the frictional force. If the trolley, when given a slight push moves down the slope with constant velocity, then the overall force down the plane is zero (no acceleration, Newton's first Law) and F (Limiting (dynamic) frictional force) = Wx.

From the diagram above:

 

giving Wy = W Cos A

 

giving Wx = W Sin A

then

Return to Thomas O'Sullivan's Homepage