
|

|
Kepler's Laws of Planetary Motion.
(Thomas O'Sullivan's Physics notes).
Johannes Kepler, (1571 - 1630) was a professor of mathematics, rhetoric astronomy and astrology in a German university who devoted his life to accurate observation of the planets' motions. He was a contemporary of Tycho Brahe (an astronomer) and Galileo and he corroborated the coppernician view of the solar system, that the earth and the other planets orbited the sun, which was in conflict with the view expressed by the Greek natural philosopher, Ptolemy, viz.; that the Earth was the centre of the universe and all heavenly bodies orbited the Earth. While attempting to predict the motion of the planet Mars he formulated his laws of planetary motion. He was one of the first astronomers to use a telescope.
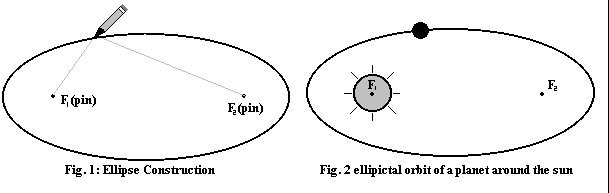
Law 1: A planet revolves around the sun in an elliptical path, with the sun at one focus of the ellipse (Fig. 2). An ellipse is an oval shaped, closed curve. An ellipse can be drawn by taking a string, tied to two pins as in the diagram and placing a pencil against the string so that the string is always taut. The path that the pencil is confined to move in is elliptical. Kepler realised from his observations that the path of the planets was also an ellipse but it took Newton in the 17th century to explain why, using his gravitational theory.
Law 2
: If a line is drawn from the centre of the planet to the centre of the sun, it sweeps out equal areas in equal time intervals. This is illustrated in fig. 3. A1, A2, A3 and A4 are the areas "swept out" by the line joining the centre of the planet to the centre of the sun in t days. All these areas are equal.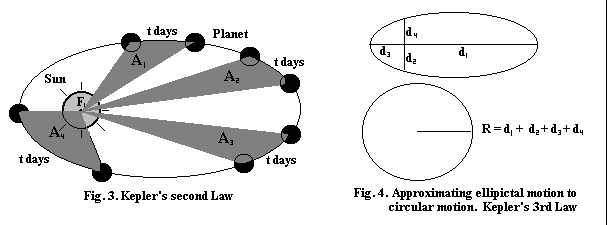
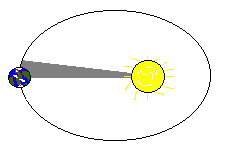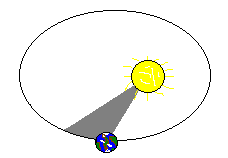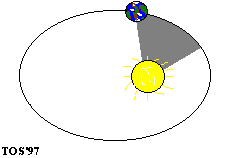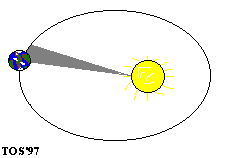
|
Law 3: If the elliptical nature of the orbit is made approximate a circle, then the square of the periodic time is directly proportional to the (mean) radius squared. Fig. 4 shows how the mean radius of the elliptical orbit is calculated. Kepler's third law is perhaps the most important of the three laws as it can be derived from Newton's Law of Gravitation and circular motion formulae.