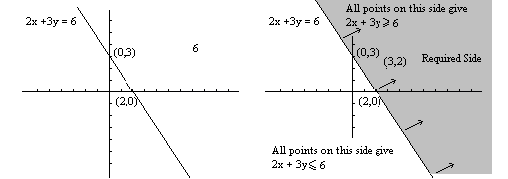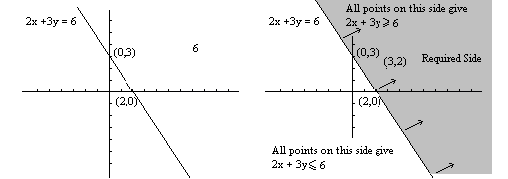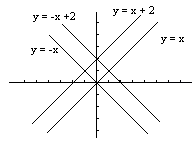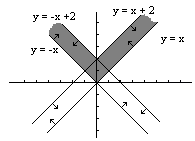|
Linear Inequalities
© Thomas O'Sullivan 1997
A line is a set of points that obey a certain condition.
e.g. 2x + 3y = 6 is "the set of points such that twice the first ordinate plus three times the second ordinate equals six". (-3,12), (0,2), (1.5,1) etc. are all points on this line as they obey the fixed condition.
A "half plane" or a "side of a line" is also a set of points that obey a certain condition.
e.g. 2x + 3y ³ 6 is "the set of points such that twice the first ordinate plus three times the second ordinate is less than or equal to six". (2,1), (2,0), (1,1), (3, -1), (0,1) etc. are all points on this "side of the line" as they all obey the fixed condition.
|
|